An Analysis of Car and Driver Impact on Formula 1 Success - Part 2

 

In the previous part of this project, I looked at the variables I was using, and some of the trends that I identified through a preliminary analysis.

Part 2 of this project is dedicated to:

 - The research questions I formulated

 - The statistical analyses that I used for each question

 - The interpretation of my analysis

 - What conclusions I was able to draw to answer each research question

Research Questions

Based on my preliminary analysis of the variables that I was working with, I came up with more questions that I was interested in exploring, in addition to my original goal of figuring out whether the car or driver was more crucial to Formula 1 success.

One of the first things that piqued my interest was how the different points systems affected overall scoring. While it was immediately clear that the change in point scoring systems from 10 points for a win to 25 points for a win resulted in drastic changes to the point totals, my hypothesis was that the change from system 1 to 2 resulted in reduced point totals for the championship winners, and created a different scoring environment between the two systems.

Research Question 1: Do the different point systems affect the scoring environment, and if so, how do they differ from each other?

To test my hypothesis out, I decided to run an ANOVA test on the points scored in relation to the points systems. My null hypothesis for the test was that there was no significant difference in the means between points systems. If there was a significant difference in the means, this would indicate that different point systems affected the scoring environment.

The results of my ANOVA test are shown below:

To interpret this ANOVA result, we must observe the p-value of the test. If the p value is less than our chosen alpha of 0.05, then we can reject the null hypothesis. In this case, the p-value of the test is nearly zero, which indicates that at least two of the scoring systems have different means, and so create different scoring environments.

The next step in my analysis of the different systems was to identify which scoring systems differed greatly in their means. To do this, I used a Tukey HSD test. The test paired each scoring system together, and compared the difference in means of each system. The adjusted p value showed how significant the difference in the means was. If the p value is less than 0.05, then there is a significant difference in the means of the two pairs of scoring systems.

The results of the Tukey HSD test are shown below:

 

Based on the Tukey HSD results, the two pairs of scoring systems that do not have a significant difference in their means are systems 1 and 2, and systems 3 and 4. While this was an expected result based on the difference in points awarded, it does leave open to interpretation the trend of championship winners gradually scoring fewer points during scoring system 2.

To answer the question, the points systems do impact the scoring environment because of the way they award points for results. Systems 1 and 2 are similar to each other in that they award fewer points for results and suppress the scoring environment, while systems 3 and 4 inflate the scoring environment in comparison to systems 1 and 2.

Research Question 2: How do pole positions in a season contribute to wins, and is the relationship between pole positions and wins similar to pole positions and points?

After I looked at the effect on points systems on scoring environment, I looked at another variable that has a slightly nebulous, but still quantifiable connection to points, pole positions achieved. While pole positions have a relatively simple and strong connection to winning, as starting from first place on the grid provides an advantage in the race, its effect on points scored is not as concrete. There are many variables that affect the total number of points scored throughout a season, and as pole positions do not contribute any points, their effect on points is limited.

My goal for this part of the analysis was to create a simple linear regression model with poles as the independent variable, and first with wins as the dependent variable, and then with points as the dependent variable.

The linear model for pole positions compared to wins is shown below:

 

From this model, we can learn a lot about how pole positions and wins are correlated to each other. Firstly, the intercept is the estimated value of the response variable (wins) when the predictor variable (poles) is zero. In this situation, this means that a driver with zero poles throughout a season can be expected to win almost one race throughout the course of the season. Next, the poles estimate is the estimated change in the response variable for a one-unit increase in the predictor variable (poles). In this case, it suggests that, on average, each additional pole is associated with an increase of approximately 0.82437 in the number of wins. This shows that pole positions greatly impact wins.

This assertion is also backed up by studying the p value. The p-value associated with the coefficient for poles is very small (very close to zero), indicating that the number of poles is significantly associated with the number of wins.

R-squared (0.6152) represents the proportion of the variance in the dependent variable (wins) that is explained by the independent variable (poles). This means that poles explain around 61.52Adjusted R-squared (0.6119) adjusts the R-squared value based on the number of predictors in the model.

In summary, the model suggests that there is a statistically significant positive relationship between the number of poles and the number of wins.

The linear model for pole positions compared to points is shown below:

From this model, we can learn a lot about how pole positions and points are correlated to each other. Firstly, the intercept is the estimated value of the response variable (points) when the predictor variable (poles) is zero. In this situation, this means that a driver with zero poles throughout a season can be expected to score around 108 points throughout the course of the season. Next, the poles estimate is the estimated change in the response variable for a one-unit increase in the predictor variable (poles). In this case, it suggests that, on average, each additional pole is associated with an increase of approximately 16 points. This shows that pole positions impact points scored, though not to the same degree as they impact wins.

The p-values associated with both the intercept and the poles coefficient are very small (nearly zero), indicating that both coefficients are statistically significant.

The multiple R-squared is 0.2354, indicating that approximately 23.54% of the variability in the dependent variable (points) is explained by the model. Adjusted R-squared is 0.2289, which adjusts the R-squared value based on the number of predictors in the model.

The F-statistic tests the overall significance of the model. In this case, it's 36.32 with a very low p-value, suggesting that the overall model is statistically significant.

In summary, the model suggests that there is a significant linear relationship between the number of "poles" and the "points" variable. The intercept and slope are both statistically significant, and the model is deemed significant based on the F-statistic. However, the R-squared value indicates that only about 23.54% of the variability in points is explained by the number of poles, which indicates that poles do not explain the variation in points scored as much as they impact winning.

To answer this research question, my hypothesis that pole positions would impact winning more than they would impact points scored was correct. This means that while pole positions can be used to predict a driver’s chances of winning a single race, they are not as accurate in predicting performance over the course of a season.

Research Question 3: Which is more instrumental to success, the car or the driver?

After finishing all my other analysis, I addressed the main point that I was hoping to answer with this research, whether the car or the driver is more influential to success. To look at the effect of the car on points, I decided to use paired t-tests to first find out whether there was a significant difference in the means of the gap in points between teammates over the course of each season.

To approximate the effect the drivers have on performance, I found the difference between the best driver in team 1 and team 2, and ran paired t-tests comparing the difference between the drivers to each set of teammates to see whether there was a significant difference in the effect that a driver had. In this case, my null hypothesis was that there was no significant difference in the means of the gap between the two teammates.

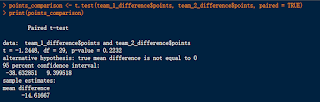
The results of my test comparing teammates are shown below:

The t-value is -1.2448. This value represents the number of standard deviations the sample mean (mean difference) is from the null hypothesis mean (0). A negative t-value suggests that, on average, team 1 has more negative points than team 2. This signifies that the gap between teammates is wider in the championship winning team than in the runner up’s team.

The p-value is 0.2232. This is the probability of observing a t-value as extreme as or more extreme than the one calculated from the sample data, assuming the null hypothesis is true. A higher p-value suggests weaker evidence against the null hypothesis. This means that the difference in the means is not significant enough to reject the null hypothesis.

The mean difference is -14.61667. This is the observed average difference in points between team 1 and team 2.

In summary, based on this analysis, there isn't sufficient evidence to conclude that there is a significant difference in mean gap between drivers in team 1 and team 2. This means that, if the cars are equal, the gap between teammates is not very different. This indicates that the car likely plays a big role in determining the number of points scored.

However, there is one interesting outlier in this analysis. The mean difference between team 1’s gap and team 2’s gap is -14.61667. This means that the gap between teammates in team 1 is higher than in team 2. This could be because many drivers’ championship winners are the best of the best, and it is difficult to find a teammate that can match up well to a championship winner.

The results of my test comparing championship rivals and team 1’s drivers are shown below:

The t-value is 3.664. This value represents the number of standard deviations by which the mean difference between the two paired sets of data differs from zero. In this case, it suggests that the mean difference is quite far from zero.

The p-value is nearly zero, which is less than the typical significance level of 0.05. This suggests strong evidence against the null hypothesis. In practical terms, it means that the observed difference in means is statistically significant.

The mean difference between the paired data sets is 27.95. This is the average change or difference observed in the sample.

In summary, the results of the paired t-test suggest that there is a statistically significant difference between the means. The positive mean difference and the confidence interval not containing zero indicate that, on average, the championship rivals’ difference is significantly higher than the teammates difference.

The results of my test comparing championship rivals and team 2’s drivers are shown below:

The t-value is 0.98846. This value represents the number of standard deviations by which the mean difference between the two paired sets of data differs from zero. A t-value close to zero indicates that the mean difference is not significantly different from zero.

The p-value is 0.3311, which is greater than the typical significance level of 0.05. This suggests that there is not enough evidence to reject the null hypothesis that there is no significant difference between the means.

The mean difference between the paired data sets is 13.33. This is the average change or difference observed in the sample.

In summary, the results of the second paired t-test suggest that there is not enough evidence to conclude that there is a statistically significant difference between the means. The p-value is greater than 0.05, and the confidence interval includes zero, indicating that we do not have strong evidence to reject the null hypothesis of no difference.

The results of these two t-tests are very interesting. They are both contradictory to each to each other, with one indicating that the driver’s ability plays a bigger role in performance, while the other test agrees that the car’s performance is more influential in performance.

My hypothesis is that this is caused because of the larger gap between the championship winner and their teammate. Because their performance is harder to replicate, it is essentially an outlier in terms of driver ability, and the interaction with the best driver often being in the best car causes the data to be skewed.

Conclusion

In summary, this project uncovered valuable insights into the interaction between various metrics, including pole positions, wins, points, and even teammate performance. The project also found out about the way car-driver interaction, especially in terms of the best driver being in the best car, can affect rigorous statistical analyses. I think that this research provides a strong foundation into the ways in which different aspects of Formula 1 can impact and contribute to success in the form of points scored.

In terms of points scoring systems, the different systems do impact the scoring environment. This is because of the difference in points awarded between systems. Pole positions correlate more to wins than points scored in a season. Pole positions are a good indicator of race winning ability, but they do not correlate much to consistency over the entire season. In terms of car-driver interaction, the results are often skewed by the fact the best driver is usually in the best car, and further research is required to account for this factor.

In terms of further research, I think that more in-depth research is needed with regards to car-driver interaction, and how that can potentially boost the contributions of both the driver and the car to success. Additionally, I think that using more advanced metrics like the AWS data insights could also provide a clearer picture of how the car and driver affect success and contribute to each other.